Nonlinear Control of an Inverted Pendulum by Partial Feedback Linearization

February 27, 2021

within the course of Nonlinear Control, I was intended to simulate the result of this paper, “Velocity and Position Control of a Wheeled Inverted Pendulum by Partial Feedback Linearization”, via MATLAB. Considering the inverted pendulum is an underactuated system, it is demanding to control such a nonlinear underactuated system, because there are less controllabe states than total states of the system.

inverted pendulum model

As we know that Feedback Linearization is a technique for transforming the main system to a simpler form, in this case, first we derive the dynamic equations of the system, next we partially feedback linearize the system, Finally apply the controller.

Dynamic Model

$M ( q ) \ddot{q} + V ( q , q _ ) = E ( q )\tau + A^T ( q ) \lambda; \mathbf{(1)}$

Eliminate Lagrange multipliers $\lambda$ with $S^T$:

$( S^T MS )\dot{\nu} + S^T ( M \dot{S}\nu + V ( q , \dot{q})) = S^{T} E ( q )\tau ; \mathbf{(2)}$

$https://latex.codecogs.com/svg.image?\nu = [\dot{\alpha},v,\dot{\theta}]^T$

Then the input-affine form of equations:

$\dot{x} = f ( x ) + g ( x ) u; x=\begin{pmatrix} q_r \\ \nu\end{pmatrix};\mathbf{(3)}$

$g ( x ) =[g_1(x), g_2(x)]= \begin{pmatrix} 0_{4*2} \\ (S^T M S)^{-1} S^T E\end{pmatrix}_{7*2} ; u=\begin{pmatrix} \tau_r \\ \tau_l\end{pmatrix}; \mathbf{(4)}$

$f ( x ) =\begin{pmatrix} f_1(x) \\ f_2(x)\end{pmatrix}=\begin{pmatrix} S_r \nu \\ -(S^T M S)^{-1} S^T (M\dot{S}\nu + V(q_r, \dot{q_r}))\end{pmatrix}_{7*1} ; q_r=[x_o,y_o,\theta,\alpha]^T;\mathbf{(5)}$

And the new feedback law is:

$\omega_1=f_2[3]+v_2$

$\omega_2=f_2[1]+g_1[5]v_1; \mathbf{(6)}$

Now let’s feedback linearize the system. Considering, it has maximum relative degree, the change of coordinates is given by:

$z = T(x)=\begin{pmatrix} x_3\\ x_7\\ x_4\\ x_5\\ x_1\\ x_2\\ -x_5g_1[6]+x_6g_1[5]\\\end{pmatrix}; \mathbf{(7)}$

Finally the equations of the system become:

$\dot{z}_1=z_2, \dot{z}_2=\omega_1,\dot{z}_3=z_4,\dot{z}_4=\omega_2$

$\dot{z}_5=(\frac{z_7+g_1[6]z_4}{g_1[5]})cos(z_1)$

$\dot{z}_6=(\frac{z_7+g_1[6]z_4}{g_1[5]})sin(z_1)$

$\dot{z}_7=z_4(-z_4\frac{\partial g_1[6]}{\partial z_3}+\frac{\partial g_1[5]}{\partial z_3}\frac{z_7+g_1[6]z_4}{g_1[5]})+g_1[5](f_2[2]-f_2[1]\frac{g_1[6]}{g_1[5]}); \mathbf{(8)}$

Design and Implementation of Controllers

Velocity Controller

In order to control desired parameters of the system, we need two controllers; a lower level controller with fast dynamics to track $\theta_d$ and $\alpha_r$, and a higher level controller with slow dynamics to make sure $\lambda_r \in A_s$:

$C_l: \omega_1=-k_{qv}\dot{\theta}-k_q(\theta-\theta_d), \omega_2=-k_{av}\dot{\alpha}-k_a(\alpha-\alpha_r); \mathbf{(9)}$

$C_h: \dot{\alpha}_r=k_rf_{ss}-k_v(\alpha^2_m-\alpha^2_r)^2(v_{ss}-v_d)\frac{f_{ss}}{\alpha_r}; \mathbf{(10)}$

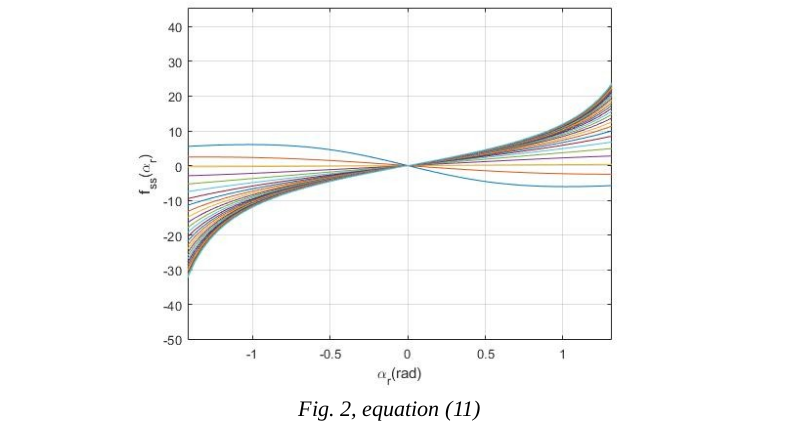
$\dot{v}_{ss}=f_{ss}(\alpha_r)=[\frac{1}{g_1[5]}(g_1[5]f^\alpha_{22}-f^\alpha_21g_1[6])]_{\alpha=\alpha_r};\mathbf{(11)}$

Simulation of equation (11):

f_ss

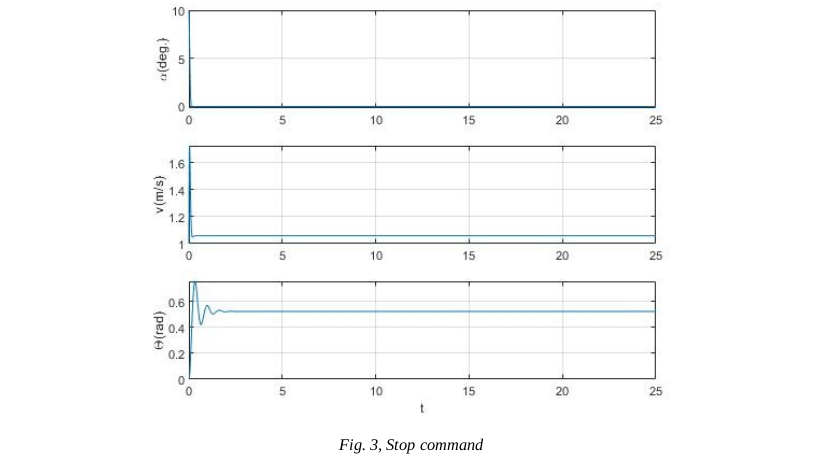
Now the outputs for step and stop commands:

stop command

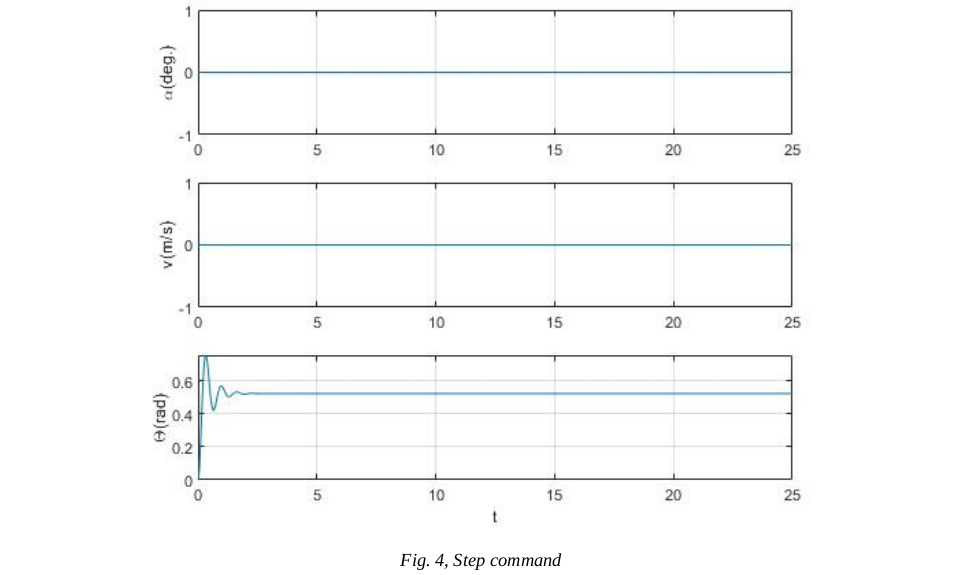
step command

Position and Stabilization Control

Here we want to design a controller to stabilize the robot in a desired coordination against the world frame. For this, it is better to deploy polar coordination for for configuration space of the robot:

$P=[\rho,\phi,\theta,\alpha ]^T;\mathbf{(12)}$

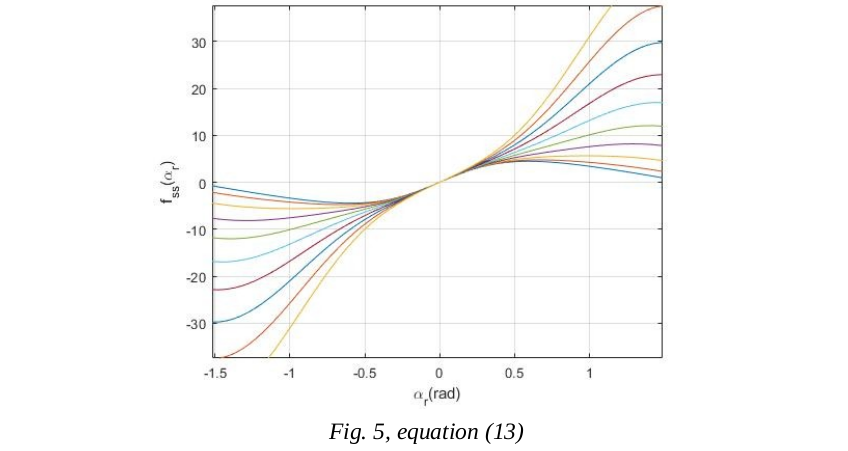
$\dot{v}_{ss}=f(\alpha_r,\dot{\theta})=\begin{bmatrix}(f^\alpha_{22}+f^{\dot{\theta}}_{22})-(f^\alpha_{21}+f^{\dot{\theta}}_{21})\frac{g_1[6]}{g_1[5]}\end{bmatrix}_{\alpha=\dot{\alpha}} ;\mathbf{(13)}$

The simulation:

f_ss_theta_dot

Same as befor we need two types of controller, higher level and lower level controllers, for higher level controller, we consider the following potential function:

$V_\Sigma=\frac{1}{2(\alpha^2_m-\alpha^2_r)}+\frac{k_v(v_{ss}-v_d)^2}{2}; \mathbf{(14)}$

We propose the following control signal:

$\omega_1=-\frac{\partial V_\Sigma }{\partial \theta}-k_\omega\dot{\theta}; \mathbf{(15)}$

Finally, by substituting $\alpha_r$ in the following equation, stability would be satisfied.

$f_{ss}(\alpha_r, \dot{\theta})=-(\frac{\partial V_\Sigma }{\partial \rho}cos(\theta-\phi)+\frac{\partial V_\Sigma }{\partial \phi}\frac{sin(\theta-\phi)}{\rho})-k_vv;\mathbf{(16)}$

And the lower level controller is:

$\omega_2=-k_{av}\dot{\alpha}-k_a(\alpha-\alpha_r);\mathbf{(17)}$

References

[1] Velocity and Position Control of a Wheeled Inverted Pendulum by Partial Feedback Linearization

To get more details, please refer to the papaer and keep in touch with me. :)