Development and Simulation of Bimanual Object Manipulation, Using UR5 Manipulators; M.Sc. Dissertation

February 12, 2023

Abstract

Manipulating an object or in more general terms, the ability of the robot to interact with its environment, for modification and enhancing that, is called “manipulation”. This has usually been done by an articulated robot equipped with a gripper. Within this research, the manipulation will be done by occupation of two articulated robotic arms, while after holding the object, the set of two robotic arms and the object make a closed dynamic chain.
The most significant aspect of optimal bi-manual manipulation against manipulation with only one articulated robotic arm is, having a better and more efficient control on manipulation. In this method, bi-manual manipulation of the object acquires dynamic models of both arms and the object. Also, in typical methods of object manipulation, it is common to measure or estimate contact forces by sensors. Due to the intrinsic complexity of the whole system dynamics, measurement of the constraint generalized forces in the contacts of object and arms needs high precision sensors and periodic calibration, also force-torque sensors have limited range, steady state error and include noise. So it is desirable to calculate them in the absence of force-torque sensors.
Analytical calculation of the inverse dynamics for a closed-chain robotic system in the absence of force-torque sensors in wrist is not easy to implement, because of the constraint term in the equation of the motion. Thanks to a method called “Orthogonal Decomposition”, the aforementioned problem is handled, though. In addition, by designing the null-space of the task, we would be able to control the squeeze and motion terms of forces for manipulation. What we want to develop in this research is according to the previous researches, but in a physics-based simulation environment, Gazebo, via two UR5 robot manipulators under some oiptimizations for constraints and trajectory planning in quaternion space.

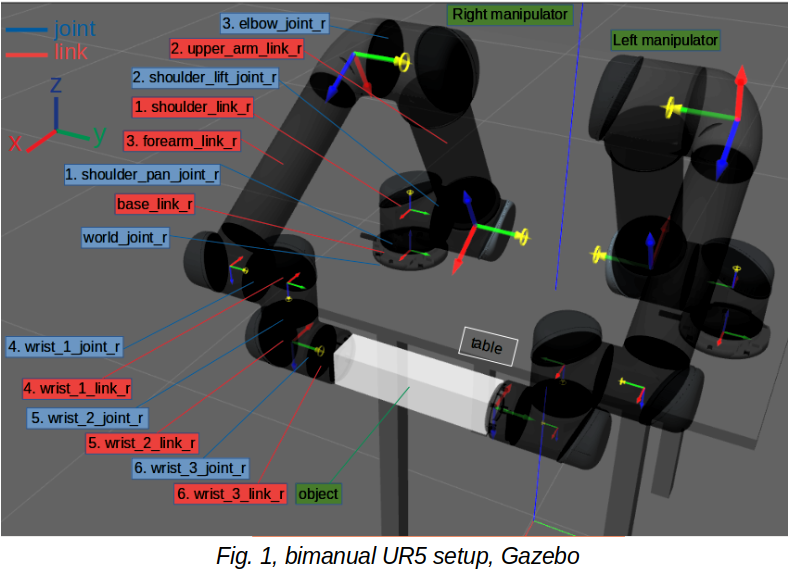
bimanual setup

Introduction, Problem Statement

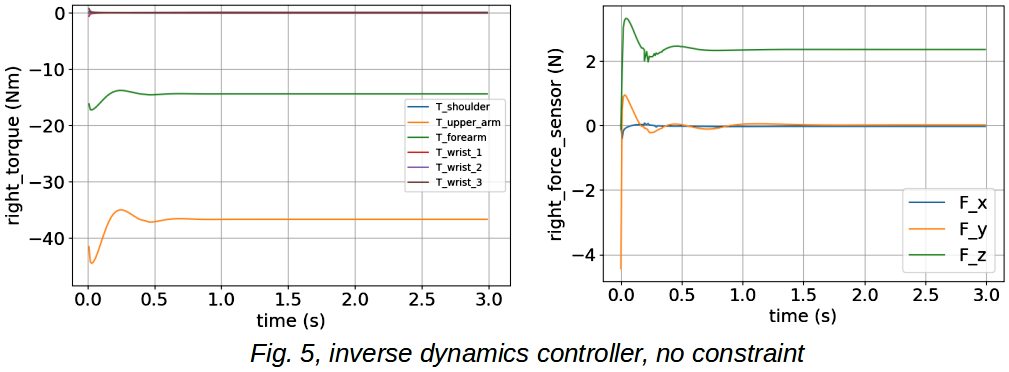
We have simulated manipulation (translational and orientational displacement) of an object by a dual arm robot, in this case; two UR5 manipulators. Simulation is done via Gazebo (v9) and ROS (Robot Operating System, Melodic); and for dynamic and kinematic calculations we leveraged RBDL. There are two controllers used in this research for manipulation, 1. inverse dynamics, 2. constrained QP (Quadratic Programming). According to the proposed inverse dynamics method, it is feasible to calculate contact (end-effector to object) force and torque in the absence of force-torque sensors, and for validation of the results, we compared it with the data measured by sensors placed in the wrist of manipulators. In addition, to avoid singularity and other limitations of Euler’s rules for orientation planning of the object, we used quaternion math for this purpose.

Architecture of Algorithm

In this section, a brief description of different parts of the algorithm is shown through diagrams.

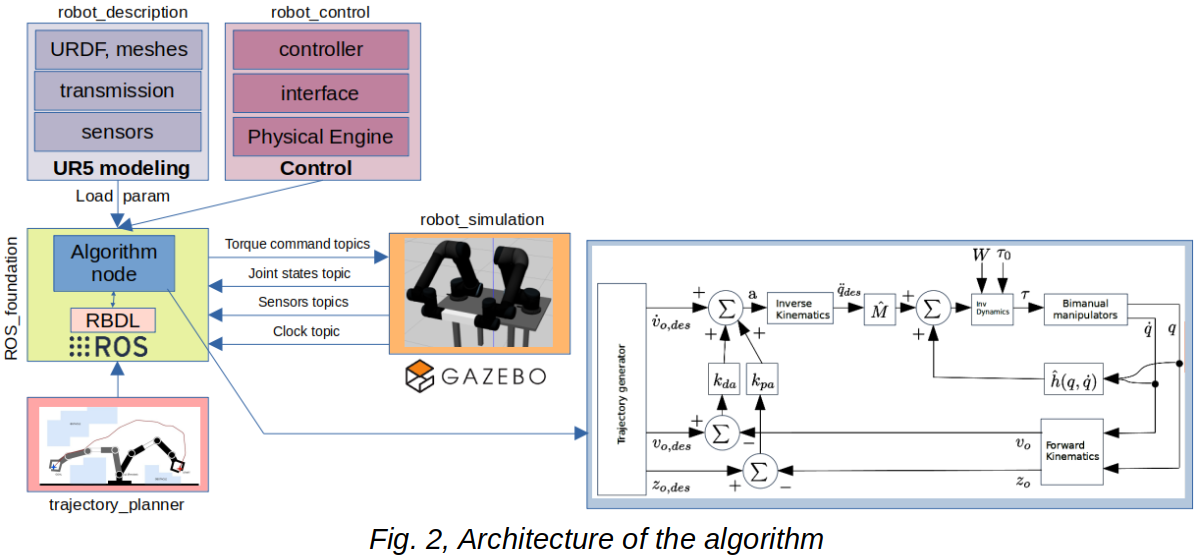
algorithm architecture

As you see in Fig.2; first, we have prepared a URDF model of UR5 manipulator. Here, it was just some modifications on the predefined validated model of the UR5. Second, the control algorithm is implemented as a ROS node. Third, the desired trajectory for the object in 3D would be interpolated for certain initial and final states of object. Forth, the algorithm receives states of the robot (joint position and velocity) from Gazebo and then calculates the desired torque for tracking desired trajectory of the manipulated object in Cartesian space iteratively. Also, the control loop of the algorithms is shown in the blue block.

Theory

In the following the fundamental formulations related to the modeling, control and calculation of torque would be presented.

$M(q)\ddot{q} + h(q, \dot{q}) = S^T\tau + J^T(q)\lambda; (1)$

$M_o(q)\dot{v_o} + h_o(z_o, v_o) = -G_o^T(z_o)\lambda; (2)$

$G_{oi}(z_o) = \begin{bmatrix} I & p_{o/i}\times \\ 0 & I \\\end{bmatrix}, G_{oi}(z_o) \in \mathbb{R}^{k \times k}, i = \{a,b\} ; (3)$

$v_o = G_{oa}^{-1}J_a\dot{q} = G_{ob}^{-1}J_b\dot{q}; (4)$

$(J_a - G_{oa}G_{ob}^{-1}J_b)\dot{q} = 0; (5)$

$J_g\dot{q} = 0, J_g \in \mathbb{R}^{k \times n}; (6)$

$\hat{M}\ddot{q} + \hat{h} = S^T\tau + J_g^T\lambda_a; (7)$

$\hat{M} = M + J_b^TG_{ob}^{-T}M_oG_{ob}^{-1}J_b; (8)$

$\hat{h} = h + J_b^TG_{ob}^{-T}(h_o + M_oG_{ob}^{-1}(\dot{J_b} - \dot{G}_{ob}G_{ob}^{-1}J_b)\dot{q}); (9)$

As you see, we could derive the whole dynamics equation of bimanual robot and object in (7) by merging bimanual robot dynamic (1) and object dynamic (2) equations via the defined Grasp Matrix (3). ‘k’ is the number of constraints per each end-effector and ‘n’ is bimanual robot degrees of freedom. The jacobian matirix in (6) is called Grasp Jacobian.
Now, lets calculate the inverse dynamics solution by “QR” decomposition of transposed grasp jacobian:

$J_g^T = \hat{Q}[\hat{R}^T 0]^T; (10)$

$P_{QR} = \hat{S}_u \hat{Q}^T, \hat{S}_u = [0_{(n-k) \times k} I_{n-k}]; (11)$

$P(\hat{M}\ddot{q} + \hat{h}) = PS^T\tau; (12)$

$\tau(W, \tau_0) = (PS^T)^{\sharp}P(\hat{M}\ddot{q}_{des} + \hat{h}) + (I - (PS^T)^{\sharp}PS^T)W^{-1}\tau_0; (13)$

$(PS^T)^{\sharp} \overset{\underset{\mathrm{def}}{}}{=} W^{-\frac{1}{2}}(PS^TW^{-\frac{1}{2}})^+; (14)$

$\lambda_a = \hat{R}^{-1}\hat{S}_c\hat{Q}^T(\hat{M}\ddot{q}_{des} + \hat{h} - S^T\tau), \hat{S}_c = [I_k 0_{k \times (n-k)}]; (15)$

By pre-multiplying (11) by (7), we are able to break the dynamic equation (7) into a constrained and unconstrained (12) equations; now, the inverse dynamics would be calculated by (13), and by substituting the calculated torque into (7), we can compute the constrained force-torque analytically (15).

To compute the required torque, it is necessary to feed the desired joint acceleration:

$\ddot{q}_{des} = \begin{bmatrix} J_g \\ G_{ob}^{-1}J_b\end{bmatrix}^+(\begin{bmatrix} 0 \\ a\end{bmatrix} - \begin{bmatrix} \dot{J}_g \\ G_{ob}^{-1}(\dot{J}_b - \dot{G}_{ob}G_{ob}^{-1}J_b)\end{bmatrix}\dot{q}); (16)$

$a = \dot{v}_{o,des} + k_{da}(v_{o,des} - v_o) + k_{pa}(z_{o,des} - z_o); (17)$

Trajectory Planning

To plan the desired translational and orientational trajectory for the object, we used quintic polynomial interpolation. For translational trajectory, it is straight forward to calculate, and for orientational trajectory in quaternion space, it is the same method presented in this paper.

In the following, manipulation is done for different trajectory scenarios:

Video. 1, Bimanual manipulation, Gazebo (4 times faster)

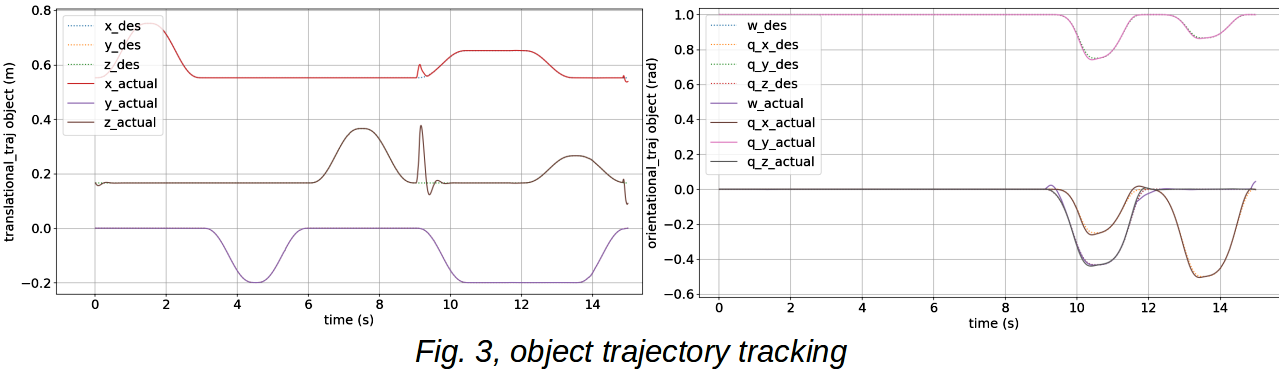
And the diagrams for the above trajectory tracking of the object are:

object trajectory tracking

Quadratic Programming Oprimization

If we want to constrain parameters like torque of motors, contact force-torque and etc, due to some inequality constraints such as maximum torque (motor stall), we are unable to solve the inverse dynamics problem analytically anymore, unless we handle it through optimizing a linear and quadratic cost function which includes all the constraints and dynamics.

$\frac{1}{2}\tau^TW_{\tau}\tau + b_{\tau}^T\tau + \frac{1}{2}\lambda^TW_{\lambda}\lambda + b_{\lambda}^T\lambda; (18)$

$\frac{1}{2}\tau^T(W_{\tau} + SW_cS^T)\tau + (b_{\tau}^T - (M\ddot{q} + h)^TW_cS^T - b_c^TS^T)\tau; (19)$

In accordance with this paper, it is possible to optimize both contact constraints and torque commands simultaneously with a cost function only depends on torque commands (19) with the help of dynamic redundacy of the bimanual robot. Also, inequality constraints of $A\tau \lt a$ and $B\lambda \lt b$ could be reshaped to constraints depicted below:

$PS^T\tau = P(\hat{M}\ddot{q}_{des} + \hat{h}); (20)$

$A\tau \leqslant a; (21)$

$-BR^{-1}Q_c^TS\tau \leqslant b - BR^{-1}Q_c^T(M\ddot{q}_{des} + h), Q_c^T = S_cQ^T; (22)$

For contact constraints, contact forces are within a linearized friction cone. In the following, manipulation under various constraints and object mass are shown, it is done for zero motion.

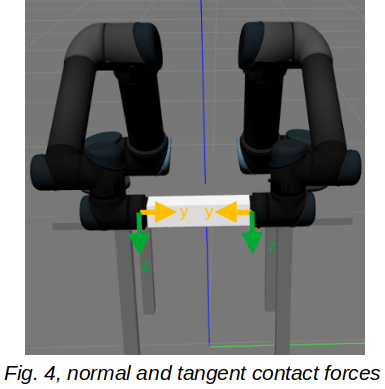
normal and tangent constraint forces

Now we want to analyze operation of the QP controller under different masses of object and constraints for torque commands and contact forces, diagrams are shown for only right manipulator, the left one is similar to some extent.

no constraint, typical inverse dynamic controller

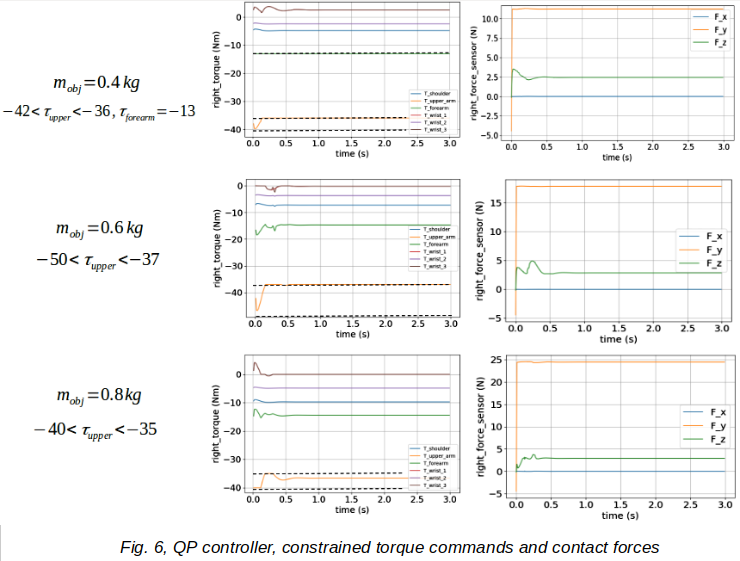
apply constraints, QP controller

As you see in fig. 6, QP controller increases normal force ($F_y$) to hold the object, while its mass increases and also satisfy constraint conditions. Contact forces are measured via force sensors, placed in the wrist of UR5 manipulators.

Appendix

This project aimed to be open-source, considering all the drawbacks and ambiguities, it is better to take a look at the source code repository and check what seems unclear. (link)

References

[1] Inverse Dynamics Control of Bimanual Object Manipulation Using Orthogonal Decomposition: An Analytic Approach
[2] A Unified Approach for Inverse and Direct Dynamics of Constrained Multibody Systems Based on Linear Projection Operator: Applications to Control and Simulation
[3] Inverse Dynamics Control of Floating Base Systems Using Orthogonal Decomposition
[4] Optimal distribution of contact forces with inverse-dynamics control
[5] Orientation Planning in Task Space Using Quaternion Polynomials
[6] On the Orientation Planning with Constrained Angular Velocity and Acceleration at Endpoints